Answer to Question #125301 in Analytic Geometry for Samuel kassapa
Question #125301
Find the area of the region inside both the rose r =sin(2Φ) and the circle r=cosΦ.The appropriate graph and intervals to the best of your interest to solve this question Expert's answer
"\\sin(2\\phi)=\\cos(\\phi)"
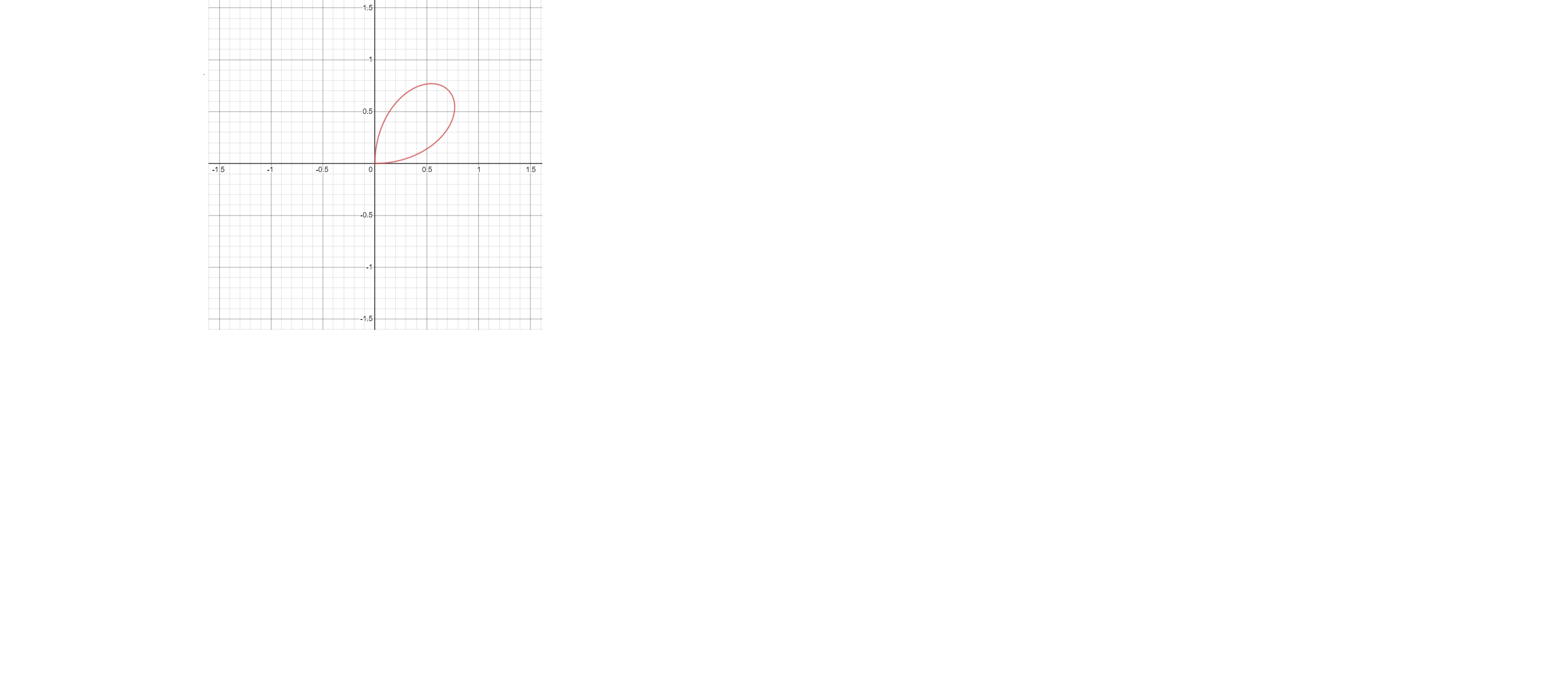 "A_1={1\\over2}\\displaystyle\\int_{0}^{\\pi\/2}(\\sin(2\\phi))^2d\\phi="
"A_1={1\\over2}\\displaystyle\\int_{0}^{\\pi\/2}(\\sin(2\\phi))^2d\\phi="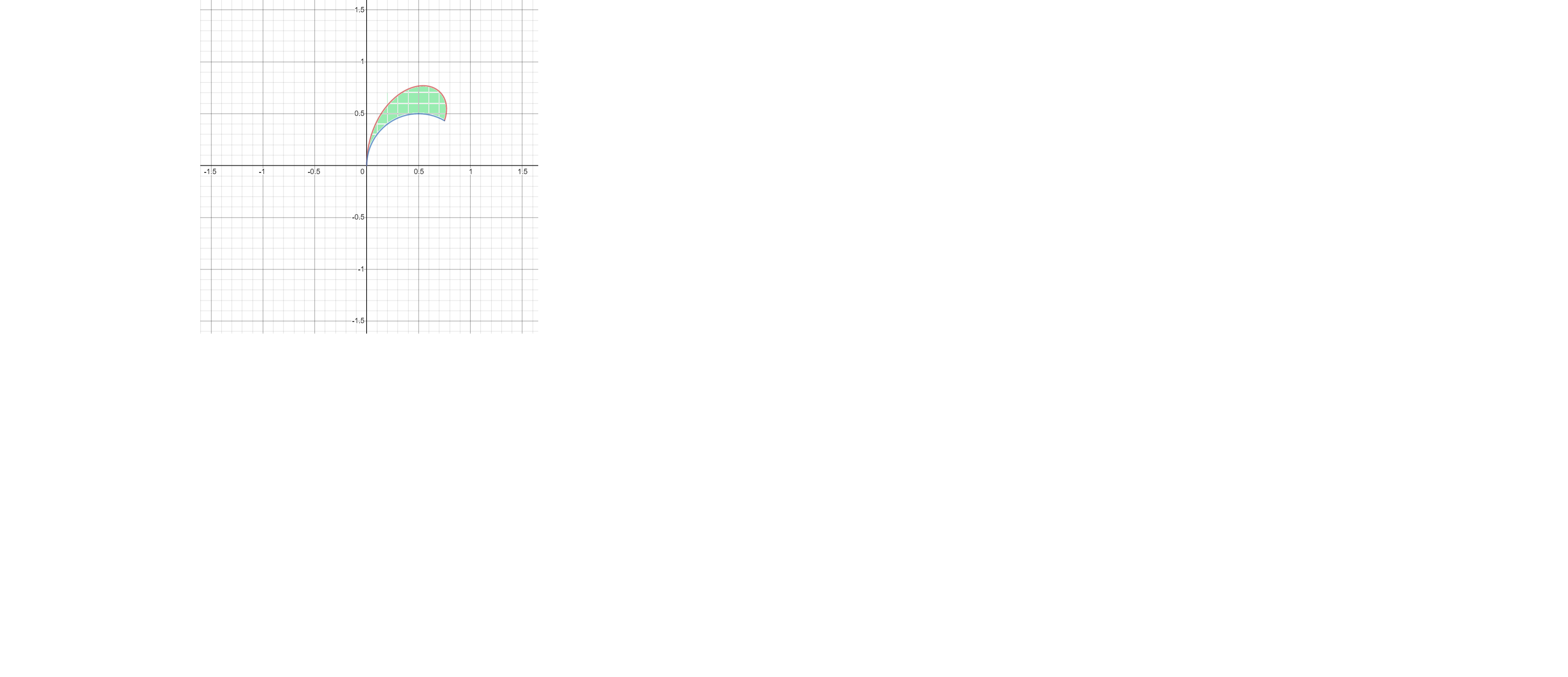 "A_2={1\\over2}\\displaystyle\\int_{\\pi\/6}^{\\pi\/2}\\bigg((\\sin(2\\phi))^2-(\\cos\\phi)^2\\bigg)d\\phi="
"A_2={1\\over2}\\displaystyle\\int_{\\pi\/6}^{\\pi\/2}\\bigg((\\sin(2\\phi))^2-(\\cos\\phi)^2\\bigg)d\\phi="
"2\\sin(\\phi)\\cos(\\phi)=\\cos(\\phi)"
"\\cos(\\phi)=0\\text{ or } \\sin(\\phi)={1\\over 2}"
"={1\\over4}\\displaystyle\\int_{0}^{\\pi\/2}((1-\\cos(4\\phi))d\\phi="
"={1\\over4}\\big[\\phi-{1\\over 4}\\sin(4\\phi)\\big]\\begin{matrix}\n \\pi\/2 \\\\\n 0\n\\end{matrix}={\\pi\\over 8}(units^2)"
"={1\\over4}\\displaystyle\\int_{\\pi\/6}^{\\pi\/2}\\bigg(1-\\cos(4\\phi)-1-\\cos(2\\phi)\\bigg)d\\phi="
"=-{1\\over4}\\bigg[{1\\over 4}\\sin(4\\phi)+{1\\over 2}\\sin(2\\phi)\\bigg]\\begin{matrix}\n \\pi\/2 \\\\\n \\pi\/6\n\\end{matrix}="
"=-{1\\over4}(0-{\\sqrt{3}\\over 8}+0-{\\sqrt{3}\\over 4})={3\\sqrt{3}\\over 32}(units^2)"
"Area=\\dfrac{4\\pi-3\\sqrt{3}}{16} \\text{ square units}"
Learn more about our help with Assignments: Analytic Geometry








Comments
Leave a comment