Answer to Question #269503 in Algebra for Maheshi
Question #269503
2. The functionsf and g are defined as below. f(x) = 3x+2: XER g(x)= 6 2x +3 Find the value of x for which f(g(x)) = 3 Sketch in a single diagram, the graphs of f(x) and f(x). Express each of f(x) and g(x), and solve the equation f¹(x) = g(x)
Expert's answer
"f(x)=3x+2, x\\in \\R"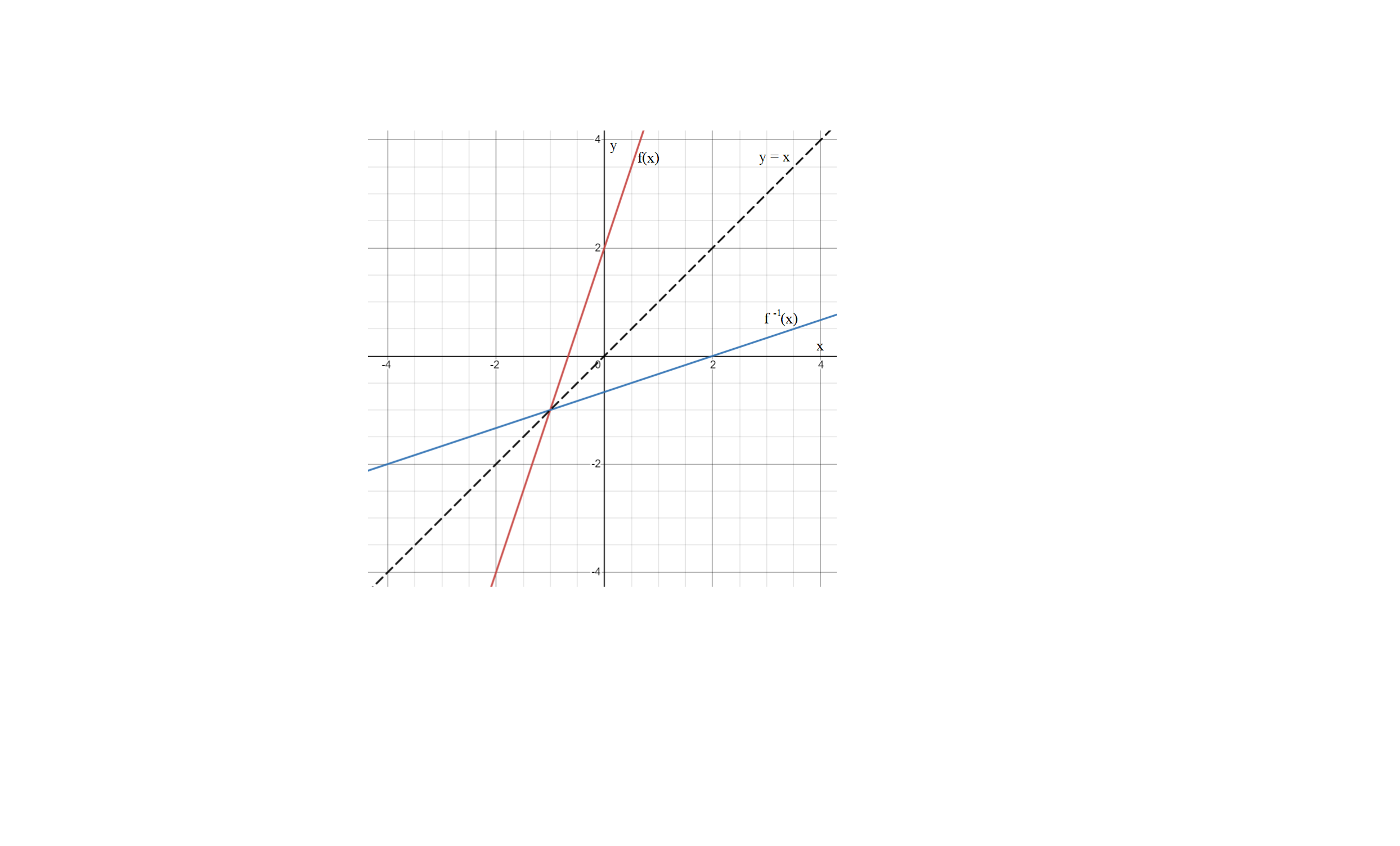
"g(x)=\\dfrac{6}{2x+3}, x\\in \\R, x\\not=-1.5"
(i)
"f(g(x)) =3(\\dfrac{6}{2x+3})+2"Given
"f(g(x)) =3""3(\\dfrac{6}{2x+3})+2=3"
"\\dfrac{18}{2x+3}=1"
"2x+3=18"
"2x=15"
"x=7.5"
(ii)
Replace "f(x)" with "y"
Interchange "x" and "y"
Solve for "y"
Replace "y" with "f^{-1}(x)"
The graph of a function and its inverse are symmetric with respect to the line "y=x."
(iii)
Replace "g(x)" with "y"
Interchange "x" and "y"
Solve for "y"
"2y=\\dfrac{6}{x}-3"
Replace "y" with "g^{-1}(x)"
Given
"\\dfrac{1}{3}x-\\dfrac{2}{3}=\\dfrac{3}{x}-1.5"
"x^2-2x=9-4.5x"
"x^2+2.5x-9=0"
"D=(2.5)^2-4(1)(-9)=42.25"
"x=\\dfrac{-2.5\\pm\\sqrt{42.25}}{2(1)}=-1.25\\pm3.25"
"x_1=-1.25-3.25=-4.5, x_2=-1.25+3.25=2"
"x\\in\\{-4.5, 2\\}"
Learn more about our help with Assignments: AlgebraElementary Algebra





Comments
Leave a comment