Answer to Question #283572 in Differential Equations for Palli

Question

Find orthogonal trajectory to the curve given by 𝑟 = 𝑎(1 + cos 𝜃)

Answer 1

$$r = a(1 + \cosθ)$$

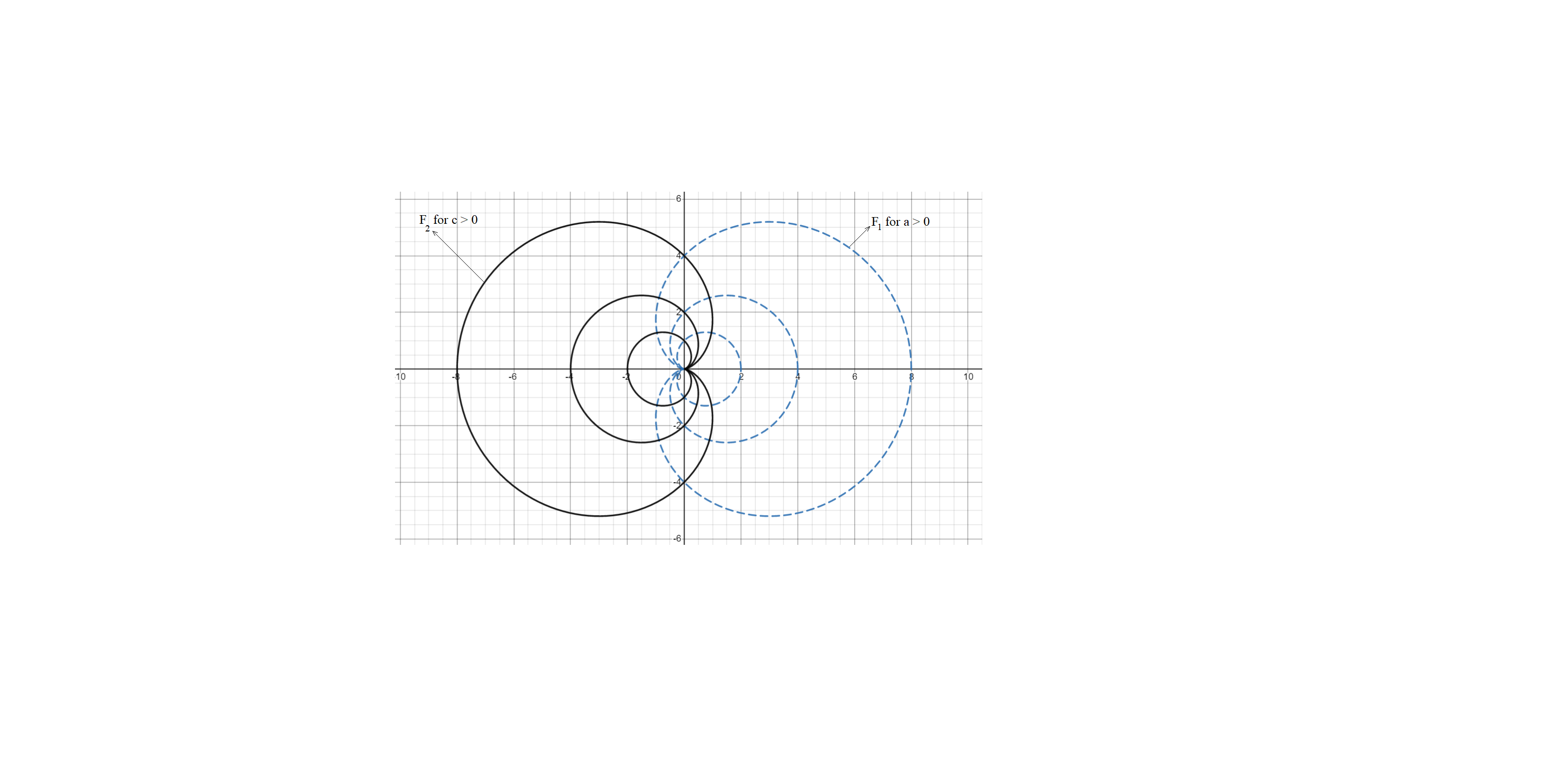
Differentiate

$$dr=-a\sin \theta d\theta$$

$$a=\dfrac{r}{1+\cos \theta}$$

$$dr=-\dfrac{r}{1+\cos \theta}\sin \theta d\theta$$

$$-\dfrac{1}{r}\dfrac{dr}{d\theta}=\dfrac{\sin \theta}{1+\cos \theta}$$

This is the differential equation of the direction field $D_1$ for the given family $F_1.$ To find the differential equation of the direction field orthological to $D_1,$ we replace $\dfrac{dr}{d\theta}$ by $-r^2\dfrac{d\theta}{dr}.$

The differential equation for the orthogonal trajectories becomes

$$r\dfrac{d\theta}{dr}=\dfrac{\sin \theta}{1+\cos \theta}=\dfrac{2\sin (\dfrac{\theta}{2})\cos (\dfrac{\theta}{2})}{2\cos^2 (\dfrac{\theta}{2})}=\tan(\dfrac{\theta}{2})$$

which is a case of variable-separable, and on integration gives

$$\ln r=2\ln(\sin(\dfrac{\theta}{2}))+\ln(2c)$$

This is the equation of the orthogonal family $F_2.$

Since $r = c(1 – \cosθ)$ represents the same curve as $r = c(1 + \cosθ),$ the member of $F_2$ with label $c$ is the same as the member of $F_1$ with label $a = –c.$ Thus the given family is selforthogonal.