Answer to Question #301372 in Calculus for Neeraj
Question #301372
The equation for a distance, s(m), travelled in time t(s) by an object starting with an initial velocity u(ms-1) and uniform acceleration a(ms-2) is: π =π’π‘+12ππ‘2 The tasks are to: a) Plot a graph of distance (s) vs time (t) for the first 10s of motion if π’=10ππ β1 and π=4ππ β2. b) Determine the gradient of the graph at π‘=2π and π‘=6π . c) Differentiate the equation to find the functions for i) Velocity (π£=ππ ππ‘) ii) Acceleration (π=ππ£ππ‘=π2π ππ‘2) d) Use your result from part c to calculate the velocity at π‘=2π and π‘=6π . e) Compare your results for part b and part d.
Expert's answer
"s(t)=10t+\\dfrac{4t^2}{2}, m"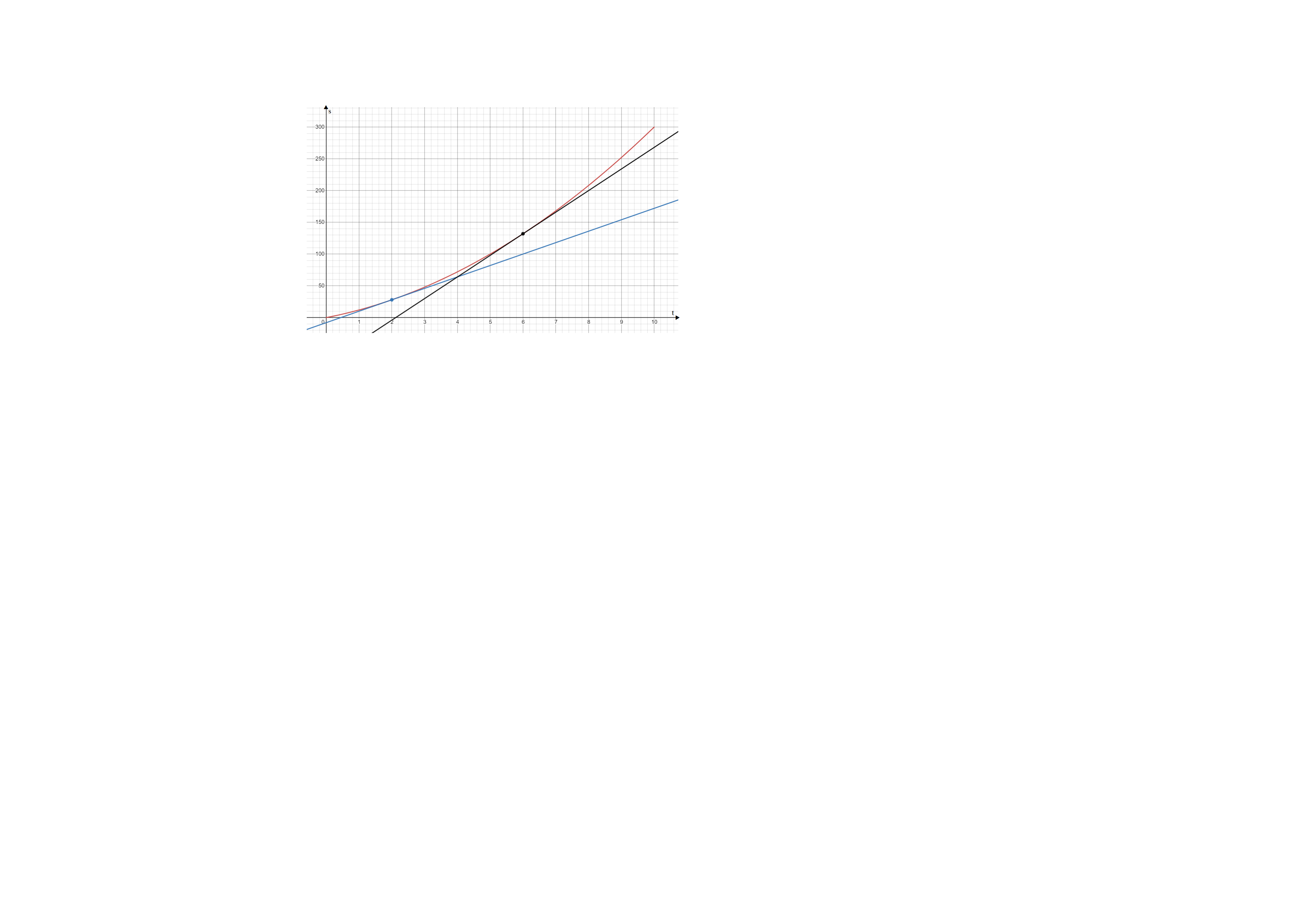
a)
b)
"t=2 , s(2)=28"
"=18+2\\Delta t\\to 18( m\/s)"
"t=6 , s(6)=132"
"=34+2\\Delta t\\to 34( m\/s)"
c)
i)
ii)
d)
"v(6)=10+4(6)=34(m\/s)"
e) The results are the same.
Learn more about our help with Assignments: CalculusPre-CalculusDifferential CalculusMultivariable Calculus








Comments
Leave a comment